Spatial and Temporal Filtering for Noise Reduction in
Fluorescence Image Sequences of Cardiac Excitation
By
Jyotsna Somayajula
Cardiac arrhythmias are disturbances in the rate or pattern of propagation of the electrical impulses (action potentials) in the heart, which trigger cardiac muscle contraction. Mapping these conduction patterns has been an important tool for understanding the mechanisms of many arrhythmias. A new optical technique using a voltage-sensitive fluorescent dye provides a sequence of images representing the membrane potentials across the surface of the heart. However, the action potentials gathered using this method are typically noisy, making it difficult to extract key features reliably. The goal of this project was to reliably extract the spatial distributions of important features from optical action potential maps, such as time of activation, peak and time of repolarization. Using these features, maps that illustrate the conduction patterns were developed. This was accomplished in two steps: (1) initial spatial and temporal filtering; and (2) automation of the feature extraction from the processed action potentials.

The time series at each pixel in the heart image is an inverted representation of an action potential. This signal is normalized by calculating the percent change in fluorescence compared to the average baseline or resting potential.
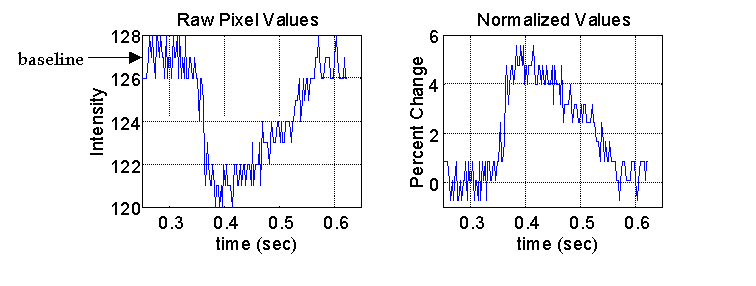
The raw pixel values and the normalized action potential for the same pixel are shown in below. This gives a temporal representation of the local activation at each pixel in the heart image.
Phase-shift Spatial Filtering
Taking into account that the morphology of the raw signals within a local neighborhood of pixels varies quite modestly, we concluded that spatial averaging would provide an effective means of noise reduction. However, the situation was complicated by the fact that the signal was not only varying in time, but was also moving as a wavefront, varying in space. The wave is propagating through the rabbit heart at a rate between 200 mm/sec and 800 mm/sec under normal, unstressed conditions. The average adult rabbit heart is 20 mm along the short axis and 30 mm along the long axis. The average imaging ratio is 86 pixels for 30 mm, using a camera speed of 400 frames/sec. At this speed, the wave can shift between 0.2 frames/pixel to 0.7 frames/pixel. Failing to correct for this shift would result in a blurring of the signal and loss of key features such as the sharp upstroke of depolarization.
Therefore, we employed a phase correlation technique to correct for this time shift prior to performing any spatial filtering. The phase correlation method is often used to compute the shift in time signals collected by a sensor array, and the principle behind the technique is as follows.
Let ![]() be the time-shifted version of
be the time-shifted version of ![]() :
:
![]()
Taking the Fourier transform of both sides, we obtain:
![]() .
.
And therefore
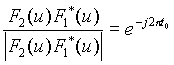
Taking the inverse transform will give an impulse function, which is centered at the shift, ![]() .
.
The spatial averaging was performed on a 5 x 5 pixel neighborhood of the image. The signal from the center pixel was used as a matched filter, and the phase shift values for the surrounding 24 optical action potentials were calculated using the method described above. All of the action potentials were interpolated in time by a factor of 10 so that sub-frame phase shifts could be resolved. The signals from the surrounding pixels were then shifted to be in phase with the center pixel, and a 5 x 5 Gaussian convolution kernel (s = 0.625) was applied to perform the averaging.
To evaluate the quality of the filtering process, 30 raw optical action potentials were randomly sampled from 4 different hearts. For each of the signals, an ideal was manually developed with effort taken to preserve the critical features of the signal. An example is shown below. The mean squared error (MSE) between the ideal and the processed signal was used as a measure of quality of the filtering process.
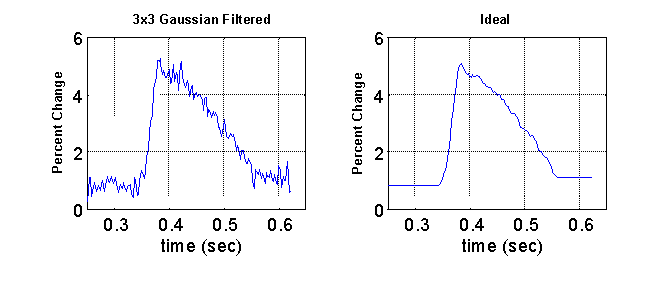
Table 1 shows the average MSE values calculated from the application of three different Gaussian convolution kernels: 3 x 3 (s = 0.391), 5 x 5 (s = 0.625), and 7 x 7 (s = 0.850) with and without the phase correction. The average MSE of the raw unfiltered signal was 0.3888. Without the phase correction, the 3 x 3 filter resulted in a modest improvement in signal quality, but application of the larger sized filters resulted in a degradation of signal quality due to the blurring effects discussed previously. Incorporating the phase correction resulted in a dramatic improvement of signal quality with all three kernel sizes. The best signal quality was achieved with the 5 x 5 filter which resulted in an average MSE of .0234, an improvement over the unfiltered signal by a factor of 17.
|
|
Unfiltered |
3 X 3 |
5 X 5 |
7 X 7 |
|
Unprocessed Data |
0.3888 ± 0.1614 |
0.2876 ± 0.1036 |
0.4654 ± 0.1307 |
0.5711 ± 0.1620 |
|
Phase-shifted Data |
0.3888 ± 0.1614 |
0.0654 ± 0.0155 |
0.0234 ± 0.0051 |
0.0531 ± 0.0081 |
Table 1: Average mean squared errors computed following the application of three different sized Gaussian convolution kernels with and without phase correction. Values were calculated from 30 optical action potentials randomly sampled from 4 different hearts.
Temporal Filtering
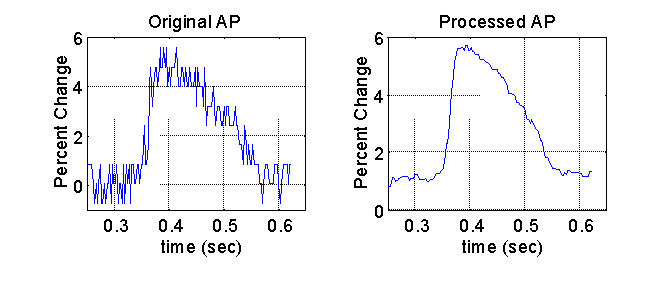
After the signals were spatially filtered, the signal quality was further enhanced with the application of a median 5 temporal filter. The median filter was specifically chosen because it preserves the steep upstroke of the optical action potential, a key feature in determining the activation time. A representative plot of the final filtered signal and the original signal is shown below.
Feature Extraction
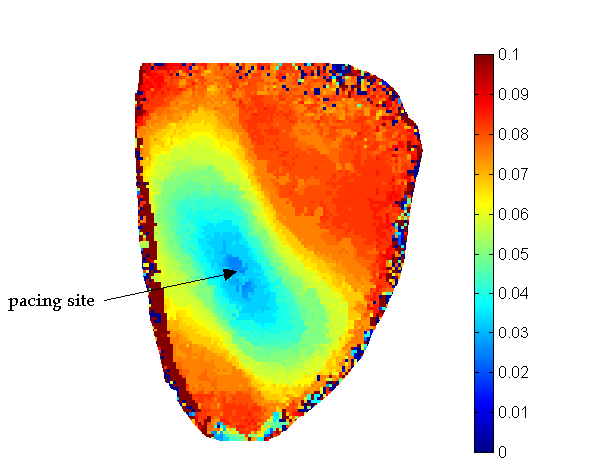
Once the images were sufficiently filtered, we were able to extract and map key features from the optical action potentials. The activation times were identified as the time at the maximum first derivative of the action potential upstroke. Prior to calculating activation time, the signals were again interpolated by a factor of 10 to attain sub-frame resolution of activation time. Action potential repolarization was calculated by determining the time at which the optical action potential had recovered to 80% of its peak value. A map of the activation times in an unstressed heart is shown in the image below. This image shows the wavefront moving outward from where the heart was probed, at the midwall of the left ventricle. Since the patterns are elliptical this image also shows that the conduction is faster in the longitudinal direction than in the transverse direction, as expected physiologically.